Question

【题目】已知曲线C的极坐标方程是.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 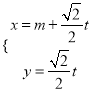(是参数).

(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线的参数方程化为普通方程;

(Ⅱ)若直线l与曲线C相交于A、B两点,且,试求实数m的值.

Answer 1

【答案】（1）（2）1或3

解： (I)曲线C的极坐标方程是化为直角坐标方程为:

直线的直角坐标方程为:

(Ⅱ)解法一:由(1)知:圆心的坐标为(2,0),圆的半径R=2,

圆心到直线l的距离

或

解法二:把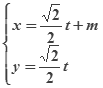(是参数)代入方程,

得,

.

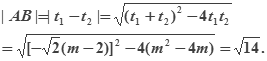
或

【解析】试题分析：利用， ，把极坐标方程化为直角坐标方程；消去参数t把直线的参数方程化为普通方程，解决圆的弦长问题有两种方法，第一直接利用圆的弦长公式，借助勾股定理去求，另一种方法是利用直线的参数方程t 的几何意义去求，把直线的参数方程带入代入到圆的直角坐标方程中，利用根与系数关系求出，借助直线的参数方程中参数的几何意义，借助，求出结果.

试题解析：

(I)曲线C的极坐标方程是 化为直角坐标方程为:

直线的直角坐标方程为:

(Ⅱ)解法一:由(1)知:圆心的坐标为(2,0),圆的半径R=2,

圆心到直线l的距离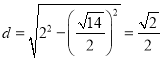

, ,

或.

解法二:把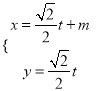 (是参数)代入方程,

得 ,

.

或.