题目内容
如图，在平行六面体ABCD-A1B1C1D1中，AB=4，AD=3，AA1=5，∠BAD=90°，∠BAA1=∠DAA1=60°．
（1）求AC1的长；
（2）设直线AC1与平面A1DB交于点G，求证：AG=
| 1 | 3 |
分析：（1）由
=
+
+
，知|
|2=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
=85，由此能求出AC1的长．
（2）由A，G，C1三点共线知，存在λ∈R，使得
=λ
=λ(
+
+
)=λ
+λ
+λ
．由B，D，A1，G四点共面知，存在x，y，z∈R，使得
=x
+y
+z
，且x+y+z=1，由此能够证明AG=
AC1．
| AC1 |
| AB |
| AD |
| AA1 |
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
（2）由A，G，C1三点共线知，存在λ∈R，使得
| AG |
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AG |
| AB |
| AD |
| AA1 |
| 1 |
| 3 |
解答：（1）解：∵
=
+
+
∴|
|2=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
=85，
∴|
|=
（2）证明：由A，G，C1三点共线知，存在λ∈R，
使得
=λ
=λ(
+
+
)=λ
+λ
+λ
由B，D，A1，G四点共面知，存在x，y，z∈R，
使得
=x
+y
+z
，且x+y+z=1
由空间向量基本定理，得x=y=z=λ，
∴λ=
，
∴
=
．
| AC1 |
| AB |
| AD |
| AA1 |
∴|
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
∴|
| AC1 |
| 85 |
（2）证明：由A，G，C1三点共线知，存在λ∈R，
使得
| AG |
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
由B，D，A1，G四点共面知，存在x，y，z∈R，
使得
| AG |
| AB |
| AD |
| AA1 |
由空间向量基本定理，得x=y=z=λ，
∴λ=
| 1 |
| 3 |
∴
| AG |
| 1 |
| 3 |
| AC1 |
点评：本题考查线段长度的求法和证明线段间的数量关系，解题时要认真审题，仔细解答，注意化空间问题为平面问题，注意向量法的合理运用．
练习册系列答案
相关题目
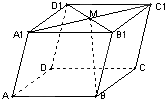如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
如图，在平行六面体ABCD-A1B1C1D1中，已知| AB |
| AD |
| AA1 |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|=|a||b|sinθ（其中θ为向量a与b的夹角），a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图，在平行六面体ABCD-EFGH中，∠EAB=∠EAD=∠BAD=60°，AB=AD=AE=2，则
如图，在平行六面体ABCD-A1B1C1D1中，若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| D1B |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
（2001•上海）如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若