题目内容
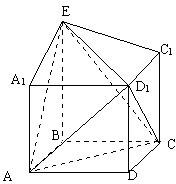 在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,
在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,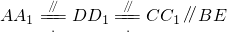 ,且AA1=AB,D1E⊥平面D1AC,AA1⊥底面ABCD.
,且AA1=AB,D1E⊥平面D1AC,AA1⊥底面ABCD.
(Ⅰ)求二面角D1-AC-E的大小;
(Ⅱ)在D1E上是否存在一点P,使得A1P∥平面EAC,若存在,求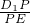 的值,若不存在,说明理由.
的值,若不存在,说明理由.
解:(Ⅰ)设AC交BD于O,建立如图所示的坐标系,
设AB=2,则 ,
, ,D1(0,1,2)
,D1(0,1,2)
设E(0,-1,t),则 ,
, ,
,
∵D1E⊥平面D1AC,∴ ,∴-2-2(2-t)=0,∴t=3,∴E(0,-1,3),
,∴-2-2(2-t)=0,∴t=3,∴E(0,-1,3),
∴
设平面EAC的法向量为 =(x,y,z),则
=(x,y,z),则 ,∴
,∴
令z=1,可得 =(0,3,1),
=(0,3,1),
∵平面FAC的法向量为
∴cos< >=
>= =
=
∴二面角D1-AC-E的平面角为45°;
(Ⅱ)设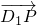 =λ
=λ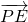 =λ(
=λ( ),则
),则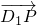 =(0,-
=(0,- ,
, )
)
∴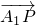 =
= +
+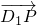 =(-
=(- ,1-
,1- ,
, )
)
∵A1P∥平面EAC,∴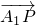 ⊥
⊥
∴ +3×
+3× +1×
+1× =0
=0
∴λ=
∴存在一点P,使得A1P∥平面EAC,此时 .
.
分析:(Ⅰ)设AC交BD于O,建立坐标系,求得E的坐标,求得平面EAC、平面FAC的法向量,利用向量的夹角公式,即可求二面角D1-AC-E的大小;
(Ⅱ)利用A1P∥平面EAC,可得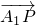 ⊥平面EAC的法向量,从而可得结论.
⊥平面EAC的法向量,从而可得结论.
点评:本题考查面面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

设AB=2,则
 ,
, ,D1(0,1,2)
,D1(0,1,2)设E(0,-1,t),则
 ,
, ,
,
∵D1E⊥平面D1AC,∴
 ,∴-2-2(2-t)=0,∴t=3,∴E(0,-1,3),
,∴-2-2(2-t)=0,∴t=3,∴E(0,-1,3),∴

设平面EAC的法向量为
 =(x,y,z),则
=(x,y,z),则 ,∴
,∴
令z=1,可得
 =(0,3,1),
=(0,3,1),∵平面FAC的法向量为

∴cos<
 >=
>= =
=
∴二面角D1-AC-E的平面角为45°;
(Ⅱ)设
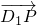 =λ
=λ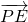 =λ(
=λ( ),则
),则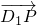 =(0,-
=(0,- ,
, )
)∴
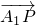 =
= +
+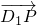 =(-
=(- ,1-
,1- ,
, )
)∵A1P∥平面EAC,∴
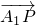 ⊥
⊥
∴
 +3×
+3× +1×
+1× =0
=0∴λ=

∴存在一点P,使得A1P∥平面EAC,此时
 .
.分析:(Ⅰ)设AC交BD于O,建立坐标系,求得E的坐标,求得平面EAC、平面FAC的法向量,利用向量的夹角公式,即可求二面角D1-AC-E的大小;
(Ⅱ)利用A1P∥平面EAC,可得
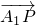 ⊥平面EAC的法向量,从而可得结论.
⊥平面EAC的法向量,从而可得结论.点评:本题考查面面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC. 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB. 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.