题目内容
已知x>1,则a=log
x,b=(
)x-1,c=(
)x从大到小的排列应为
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
b>c>a
b>c>a
.分析:由x>1,知a=log
x<log
1=0,b=(
)x-1>(
)0=1,0<c=(
)x<(
)0=1,由此能把a=log
x,b=(
)x-1,c=(
)x从大到小排列.
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
解答:解:∵x>1,
∴a=log
x<log
1=0,
b=(
)x-1>(
)0=1,
0<c=(
)x<(
)0=1,
∴b>c>a,
故答案为:b>c>a.
∴a=log
| 2 |
| 3 |
| 2 |
| 3 |
b=(
| 3 |
| 2 |
| 3 |
| 2 |
0<c=(
| 2 |
| 3 |
| 2 |
| 3 |
∴b>c>a,
故答案为:b>c>a.
点评:本题考查对数值大小的比较,是基础题.解题时要认真审题,注意对数函数和指数函数的性质的应用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目














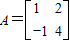
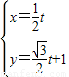 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.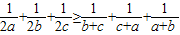 .
.

 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度. .
.