题目内容
如图所示，已知M 是双曲线
上的一点，且MF1⊥MF2，F1，F2是双曲线的两个焦点，求△MF1F2的面积．
上的一点，且MF1⊥MF2，F1，F2是双曲线的两个焦点，求△MF1F2的面积．
解：符合条件的点M 应该有4 个，分别位于第一、二、三、四象限，但无论哪种情况，△MF1F2的面积都相等，不妨设点M 在第一象限，
由已知得
，c2=40+9=49．
根据双曲线定义，得|MF1|-|MF2|=2a=
即|MF1|2+|MF2|2-2|MF1|·|MF2|=160. ①
又∵ MF1⊥MF2,
∴|MF1|2+|MF2|2=|F1F2|2 ,
即|MF1|2 +|MF2|2=(2c)2=196. ②
由①②，得
|MF1|·|MF2|=9，
∴△MF1F2的面积是9．
由已知得
，c2=40+9=49． 根据双曲线定义，得|MF1|-|MF2|=2a=
即|MF1|2+|MF2|2-2|MF1|·|MF2|=160. ①
又∵ MF1⊥MF2,
∴|MF1|2+|MF2|2=|F1F2|2 ,
即|MF1|2 +|MF2|2=(2c)2=196. ②
由①②，得
|MF1|·|MF2|=9，∴△MF1F2的面积是9．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13、如图所示，已知AP是圆O的切线，P为切点，AC是圆O的割线，与圆O交于B，C两点，圆心O在∠PAC的内部，点M是BC的中点．则∠OAM+∠APM的大小为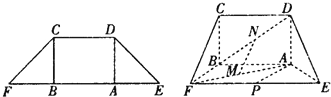
如图，在等腰梯形CDEF中，CB、DA是梯形的高，AE=BF=2，AB=2
如图所示，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点，平面PAD∩平面PBC=l．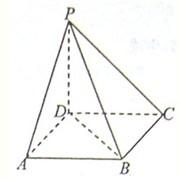
如图所示，已知ABCD是正方形，边长为2，PD⊥平面ABCD．