题目内容
已知函数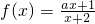
在区间（-2，+∞）上为增函数，则实数a的取值范围组成的集合为
- A.
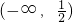
- B.
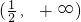
- C.
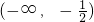
- D.
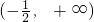
B
分析：把函数f（x）解析式进行常数分离，变成一个常数和另一个函数g（x）的和的形式，由函数g（x）在 （-2，+∞）为增函数得出1-2a＜0，从而得到实数a的取值范围．
解答：函数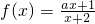=a+
，
由复合函数的增减性可知，若g（x）=在 （-2，+∞）为增函数，
∴1-2a＜0，a＞
，
故选B．
点评：本题考查利用函数的单调性求参数的范围，是基础题，解题时要认真审题，仔细解答．
分析：把函数f（x）解析式进行常数分离，变成一个常数和另一个函数g（x）的和的形式，由函数g（x）在 （-2，+∞）为增函数得出1-2a＜0，从而得到实数a的取值范围．
解答：函数
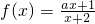=a+，由复合函数的增减性可知，若g（x）=
在 （-2，+∞）为增函数，∴1-2a＜0，a＞
，故选B．
点评：本题考查利用函数的单调性求参数的范围，是基础题，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为 
在区间[0,2]上的最小值为3，求a的值．
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为 
在区间（2，+∞）上为增函数，求实数k的取值范围。 
在区间（-2，1）上有极大值，则实数a的取值范围是（ ）