题目内容
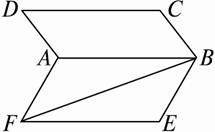
设正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角，求异面直线AD、BF所成角θ的值.
思路分析：根据题意求出两直线所在向量的数量积、两个向量的模的大小或者找出向量的数量积与两个向量的模的乘积的关系.根据cosθ=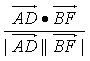
|和正方形ABEF所在平面成60°的二面角容易找到他们的关系.
解：AF⊥AB,AD⊥AB,∠FAD是两个平面所成二面角的平面角，∠FAD=60°，设正方形边长a，则BF=2a.
∵
=
=|
|·|
|·cos60°=
∴cosθ=
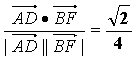,θ=arccos
.
∴异面直线AD与BF所成角为arccos
.
练习册系列答案
相关题目
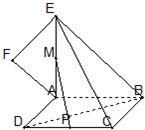如图，正方形ABCD所在平面与平面四边形ABEF所在的平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°．
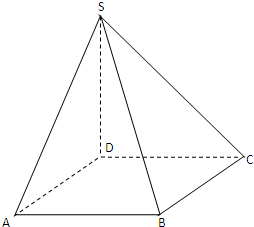如图，SD垂直于正方形ABCD所在的平面，
如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°．