Question

如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°．
（I）求证：EF⊥平面BCE；
（II）设线段CD的中点为P，在直线AE上是否存在一点M，使得PM∥平面BCE？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由；
（III）求二面角F-BD-A的余弦值．

Answer 1

分析：（Ⅰ）先证明AD，AB，AE两两垂直，再建立坐标系，证明EF⊥BE，EF⊥BC，利用线面垂直的判定，即可证明EF⊥平面BCE；
（II）证明PM⊥FE，又EF⊥平面BCE，直线PM不在平面BCE内，即可得到PM∥平面BCE；
（Ⅲ）确定平面BDF的一个法向量、平面ABD的一个法向量，利用向量的夹角公式，即可求二面角F-BD-A的余弦值．

解答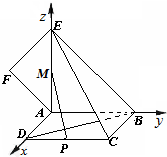：（Ⅰ）证明：因为△ABE为等腰直角三角形，AB=AE，所以AE⊥AB．
又因为平面ABEF⊥平面ABCD，AE?平面ABEF，平面ABEF∩平面ABCD=AB，
所以AE⊥平面ABCD，所以AE⊥AD．
因此，AD，AB，AE两两垂直，以A为坐标原点，建立如图所示的直角坐标系A-xyz．
设AB=1，则AE=1，B（0，1，0），D （1，0，0 ），E （ 0，0，1 ），C （ 1，1，0 ）．
因为FA=FE，∠AEF=45°，所以∠AFE=90°，从而F(0，-

1

2

，

1

2

)，
所以

EF

=(0，-

1

2

，-

1

2

)，

BE

=(0，-1，1)，

BC

=(1，0，0)．
所以

EF

•

BE

=0+

1

2

-

1

2

=0，

EF

•

BC

=0．
所以EF⊥BE，EF⊥BC．
因为BE?平面BCE，BC∩BE=B，所以EF⊥平面BCE．…（4分）
（Ⅱ）解：存在点M，当M为AE中点时，PM∥平面BCE．
M(0，0，

1

2

)，P(1，

1

2

，0)，从而

PM

=(-1，-

1

2

，

1

2

)，
于是

PM

•

EF

=(-1，-

1

2

，

1

2

)•(0，-

1

2

，-

1

2

)=0．
所以PM⊥FE，
又EF⊥平面BCE，直线PM不在平面BCE内，故PM∥平面BCE．…（8分）
（Ⅲ）解：设平面BDF的一个法向量为

n1

，并设

n1

=（x，y，z）．
∵

BD

=(1，-1，0)，

BF

=(0，-

3

2

，

1

2

)，且

n1 • BD =0 n1 • BF =0

，
∴

x-y=0 - 3 2 y+ 1 2 z=0

，取y=1，则x=1，z=3，从而

n1

=(1，1，3)，
取平面ABD的一个法向量为

n2

=(0，0，1)，∴cos＜

n1

，

n2

＞=

n1 • n2

| n1 |•| n2 |

=

3

11

=

3 11

11

．
故二面角F-BD-A的余弦为

3 11

11

．…（12分）

点评：本题考查线面垂直，考查线面平行，考查面面角，考查向量知识的运用，属于中档题．