题目内容
已知函数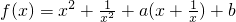
（x∈R，且x≠0）若实数a，b使得函数y=f（x）在定义域上有两个零点，则a2+b2的最小值为 ________
分析：通过换元，将函数的零点问题转化为二次函数的零点问题，换元要注意变量的范围，利用二次函数的图象求出a，b
满足的条件；利用线性规划求出a2+b2的最小值
解答：
解：令
=t（t≥2或t≤-2）则g（x）=t2+at+b
y=f（x）在定义域上有两个零点
则t2+at+b=0在（2，+∞）∪（-∞，-2）有一解
∴g（2）＜0或g（-2）＜0
即4+2a+b＜0或4-2a+b＜0
由线性规划
所以a2+b2的最小值为（0，0）到4-2a+b=0的距离的平方
故答案为：
点评：本题考查等价转化的能力、数学结合的数学方法、利用线性规划求函数的最值．
练习册系列答案
名校课堂系列答案
相关题目
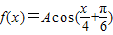，x∈R，且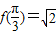
，
，
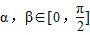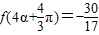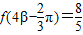，求cos（α+β）的值．
，x∈R，且
，
，
，求cos（α+β）的值．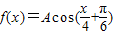
，x∈R，且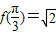
，
，
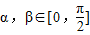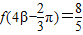，求cos（α+β）的值．
，x∈R，且
，
，
，求cos（α+β）的值．
，x∈R，且f(x)的最大值为1．
，且
，试判断△ABC的形状．