题目内容
已知向量 ,(ω∈R,ω>0),设函数
,(ω∈R,ω>0),设函数 ,若f(x)的最小正周期为
,若f(x)的最小正周期为 .
.(1)求ω的值;
(2)求f(x)的单调区间.
【答案】分析:(1)由已知中向量 ,(ω∈R,ω>0),函数
,(ω∈R,ω>0),函数 ,代入向量数量积公式,易得到函数的解析式,根据f(x)的最小正周期为
,代入向量数量积公式,易得到函数的解析式,根据f(x)的最小正周期为 ,易得到ω的值;
,易得到ω的值;
(2)根据(1)的结论,可得到f(x)的解析式,根据正弦型函数的单调性的确定方法,即可得到f(x)的单调区间.
解答:解:
=
(1)由 .
.
(2)以下均有k∈Z
令
令
所以函数的单调递增区间为 ,单调递减区间为
,单调递减区间为
点评:本题考查的知识点是正弦函数的单调性,三角函数的周期性及其求法,其中根据已知条件结合平面向量的数量积运算公式,得到函数的解析式,是解答本题的关键.
 ,(ω∈R,ω>0),函数
,(ω∈R,ω>0),函数 ,代入向量数量积公式,易得到函数的解析式,根据f(x)的最小正周期为
,代入向量数量积公式,易得到函数的解析式,根据f(x)的最小正周期为 ,易得到ω的值;
,易得到ω的值;(2)根据(1)的结论,可得到f(x)的解析式,根据正弦型函数的单调性的确定方法,即可得到f(x)的单调区间.
解答:解:

=

(1)由
 .
.(2)以下均有k∈Z
令

令

所以函数的单调递增区间为
 ,单调递减区间为
,单调递减区间为
点评:本题考查的知识点是正弦函数的单调性,三角函数的周期性及其求法,其中根据已知条件结合平面向量的数量积运算公式,得到函数的解析式,是解答本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 ,(ω∈R,ω>0),设函数
,(ω∈R,ω>0),设函数 ,若f(x)的最小正周期为
,若f(x)的最小正周期为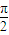 .
. ,(ω∈R,ω>0),设函数
,(ω∈R,ω>0),设函数 ,若f(x)的最小正周期为
,若f(x)的最小正周期为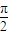 .
. ,x∈R.函数
,x∈R.函数 .
. 上的最大值和最小值.
上的最大值和最小值. ,x∈R.函数
,x∈R.函数 .
. 上的最大值和最小值.
上的最大值和最小值.