题目内容
设抛物线y2=2px(p>0)的焦点为F,直线l过点F交抛物线于A、B两点,点M在抛物线的准线上,O为坐标原点,设A(x1,y1),B(x2,y2).
(1)求证:y1y2=-p2;
(2)求证:直线MA、MF、MB的斜率成等差数列.
答案:
解析:
 ,m),
,m),
解析:
证明:
(1)设MA、MF、MB的斜率分别为k1、k、k2,A(x1,y1),?B(x2,y2),M(- 直线l的方程为:x=ty+![]() ,由
,由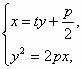 得y2-2pty-p2=0,故y1y2=-p2.
得y2-2pty-p2=0,故y1y2=-p2.
(2)由已知得y12=2px1,y22=2px2,
∴x1+![]() (y12+p2),x2+
(y12+p2),x2+![]() (y22+p2)=(y12+p2),k1+k2=
(y22+p2)=(y12+p2),k1+k2=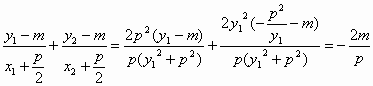 .
.
∵k=![]() ,∴k1+k2=2k.因此直线MA、MF、MB的斜率成等差数列.
,∴k1+k2=2k.因此直线MA、MF、MB的斜率成等差数列.
思路解析:本题第一问涉及直线与抛物线的交点,注意联立其方程消去一个未知数,利用根与系数间的关系从而达到目的;第二问在解决过程中注意充分利用点A、B在抛物线上这个已知条件.

练习册系列答案
相关题目
