题目内容
如图所示,正方体AC的棱长为1,该正方体内有两球相外切,并且又分别与正方体内切.(1)求两球半径之和;
(2)球的半径是多少时,两球体积之和最小?
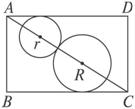
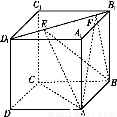
解析:(1)四边形ABCD为过球心的截面,易知它是球心的对角面,如图所示.
AC=![]() ,设两球半径分别为R、r,
,设两球半径分别为R、r,

则R+r+![]() (R+r)=
(R+r)= ![]() ,∴R+r=
,∴R+r=![]() .
.
(2)设两球体积之和为V,则
V=![]() π(R3+r3)=
π(R3+r3)=![]() π(R+r)(R2-Rr+r2)=
π(R+r)(R2-Rr+r2)=![]() π(R+r)[(R+r)2-3Rr]
π(R+r)[(R+r)2-3Rr]
=![]() π
π![]() [3R2-
[3R2-![]() ].
].
∴当R=![]() 时,V有最小值.
时,V有最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
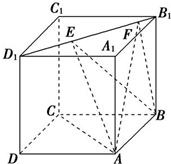 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=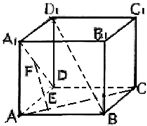 如图所示,正方体ABCD-A1B1C1D1中,EF是异面直线,AC和A1D的公垂线,则EF和BD1的关系是( )
如图所示,正方体ABCD-A1B1C1D1中,EF是异面直线,AC和A1D的公垂线,则EF和BD1的关系是( )