题目内容
已知a
R，函数
（1）当a=2时，求使f(x)=x成立的x的集合
（2）求函数y=f(x)在区间[1，2]上的最小值
解：（1）由题意f(x)=
当
时，f(x)=
，解得x=0或x=1
当
时， f(x)=
,
解得
所以所求集合为
（2）①当
，
，
，
则
区间[1，2]上的增函数，此时
②当
时，
，由
，因f(a)=0, 
③当a>2时，
，
若
，在区间（1，2）内，
，从而区间[1，2]上的增函数
若2<a<3，则
当
时，，区间[
]上的增函数
当
时，
，区间[
]上的减函数
因此2<a<3时，f(x)的最小值为a-1或4(a-2)
若
，即
，
若
，即
，
综上所述，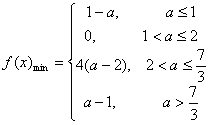
练习册系列答案
相关题目
R，b
．
及其定义域；
，若
恒成立．求实数k的取值范围．
)(x+a)(a
R).(1)若函数f(x)的图象上有与x轴平行的切线，求a的范围；(2)若
(-1)=0,(I)求函数f(x)的单调区间；（II）证明对任意的x1、x2
恒成立.
，g（x）=alnx，a
R。
（a）的解析式；
）时， 
1.
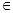R).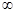
)上是增函数，求实数a的取值范围;
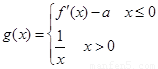，且f(x0)=3，求x0的值；
，且在R上是减函数，求实数a的取值范围。