题目内容
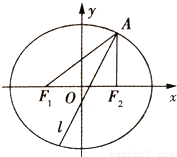
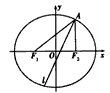
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率![]() .
.
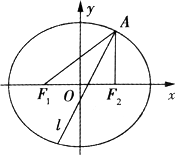
(1)求椭圆E的方程;
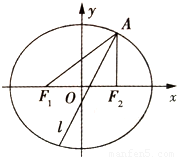
(2)求∠F1AF2的平分线所在直线l的方程;
(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
答案:
解析:
解析:
|
(1)椭圆方程E为: (2)(法一) 设角分线上任意一点为 得 (法二) (3)假设存在 方程为 在直线 BC中点为 |

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 (5分)
(5分) 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率 、
、 在x轴上,离心率
在x轴上,离心率
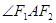 的角平分线所在直线
的角平分线所在直线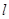 的方程.
的方程.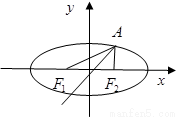
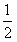 ,
,
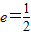 .
.
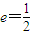 .
.