题目内容
已知z为虚数,且|z|=| 5 |
. |
| z |
分析:设z=x+yi(x、y∈R,y≠0),由条件|z|=
,z2+2
为实数求出复数z,在代入w=z+ai中,表示出|w|,即可求范围.
| 5 |
. |
| z |
解答:解:设z=x+yi(x、y∈R,y≠0)
由z2+2
=(x2+y2+2x)+(2xy-2y)i
∵z2+2
∈R,∴2xy-2y=0,
∵y≠0,∴x=1
又|z|=
,即x2+y2=5,∴y=±2,∴z=1±2i.
∵z虚部为正数,∴y=2,∴z=1+2i,
∴w=1+2i+ai
∴|w|=
,
a∈[0,1]
∴|w|∈[
,
]
由z2+2
. |
| z |
∵z2+2
. |
| z |
∵y≠0,∴x=1
又|z|=
| 5 |
∵z虚部为正数,∴y=2,∴z=1+2i,
∴w=1+2i+ai
∴|w|=
| 1+(a+2)2 |
a∈[0,1]
∴|w|∈[
| 5 |
| 10 |
点评:本题考查复数的概念、运算及复数的模等知识,设z=x+yi(x、y∈R)是复数问题中最常用的思路.

练习册系列答案
相关题目
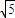 ,z2+2
,z2+2 为实数,若w=z+ai(i为虚数单位,a∈R)且z虚部为正数,0≤a≤1,求|w|的取值范围.
为实数,若w=z+ai(i为虚数单位,a∈R)且z虚部为正数,0≤a≤1,求|w|的取值范围.