题目内容
已知函数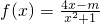
的定义域为R，且值域为（-∞，1]，求实数m的取值范围．
解：由函数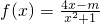的定义域为R，且值域为（-∞，1]，
∴
≤1，
∴4x-m≤x2+1，∴m≥4x-x2-1，
设y=-x2+4x-1=-（x-2）2+3，当x=2时，y取得最大值为3，
故要使m≥y恒成立，只需m≥3，
故m的取值范围为[3，+∞）．
分析：由函数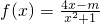的定义域为R，且值域为（-∞，1]，可得m≥4x-x2-1，设y=-x2+4x-1，只需使m≥y的最大值即可求解．
点评：本题考查了函数的值域，难度一般，关键是用配方法求函数的最值．
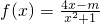的定义域为R，且值域为（-∞，1]，∴
≤1，∴4x-m≤x2+1，∴m≥4x-x2-1，
设y=-x2+4x-1=-（x-2）2+3，当x=2时，y取得最大值为3，
故要使m≥y恒成立，只需m≥3，
故m的取值范围为[3，+∞）．
分析：由函数
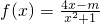的定义域为R，且值域为（-∞，1]，可得m≥4x-x2-1，设y=-x2+4x-1，只需使m≥y的最大值即可求解．点评：本题考查了函数的值域，难度一般，关键是用配方法求函数的最值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的定义域为R，且当
时，
恒成立，
对称；
图象的一个对称点。
的定义域为R，当
时，
，且对任意的实数
R，等式
成立．若数列
满足
，且
N*)，则
的值为（ ）
的定义域为R，它的反函数为
，如果
与
互为反函数，且
，则
的值为（
）
B、0
C、
D、
的定义域为R,当
时,
,且对任意的实数
R,等式
成立.若数列
满足
,且
(
N*),则
的值为（ ）