题目内容
抛物线 的焦点为
的焦点为 ,
, 在抛物线上,且
在抛物线上,且 ,弦
,弦 的中点
的中点
 在其准线上的射影为
在其准线上的射影为 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
A
解析考点:抛物线的简单性质.
分析:设|AF|=a,|BF|=b,由抛物线定义,2|MN|=a+b.再由勾股定理可得|AB|2=a2+b2,进而根据基本不等式,求得|AB|的范围,进而可得答案.
解:设|AF|=a,|BF|=b,由抛物线定义,
得AF|=|AQ|,|BF|=|BP|
在梯形ABPQ中,∴2|MN|=|AQ|+|BP|=a+b.
由勾股定理得,|AB|2=a2+b2配方得,|AB|2=(a+b)2-2ab,
又ab≤( ) 2,
) 2,
∴(a+b)2-2ab≥(a+b)2-
得到|AB|≥ (a+b).
(a+b).
所以 ≤
≤ =
= ,即
,即 的最大值为
的最大值为 .
.
故选A.

练习册系列答案
相关题目
如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A. (0,+∞) (0,+∞) | B.(0,2) | C.(1,+∞) | D.(0,1) |
若直线 经过抛物线
经过抛物线 的焦点,则
的焦点,则 的
的
最小值为( )
A. | B. | C. | D. |
设椭圆 的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6,7},则这样的椭圆的个数是 ( )
的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6,7},则这样的椭圆的个数是 ( )
| A.70 | B.35 | C.30 | D.20 |
.椭圆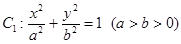 的左准线为
的左准线为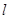 ,左、右焦点分别为
,左、右焦点分别为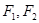 ,抛物线
,抛物线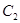 的准线也为
的准线也为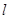 ,焦点为
,焦点为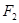 ,记
,记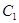 与
与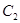 的一个交点为
的一个交点为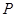 ,则
,则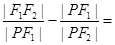 ( )
( )
A.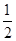 | B.1 | C.2 | D.与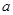 , ,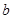 的取值有关 的取值有关 |
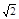
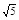
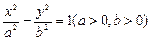 的左焦点
的左焦点 作圆
作圆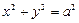 的切线,
的切线,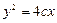 于点P,若E为线段FP的中点,则双曲线的离心率
于点P,若E为线段FP的中点,则双曲线的离心率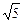
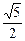

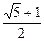
 的右焦点F作圆
的右焦点F作圆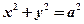 的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是( )
的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是( )
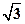
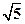
 上一点p到椭圆一个焦点的距离3,则点p到另一个焦点的距离为
上一点p到椭圆一个焦点的距离3,则点p到另一个焦点的距离为