题目内容
已知定点A（-2，
），点F为椭圆
的右焦点，点M在椭圆上移动时，求|AM|+2|MF|的最小值，并求此时点M的坐标.
解:由椭圆方程，得a=4,b=,c=2,
∴e=
,右焦点F（2，0），右准线l：x=8.
设点M到右准线l的距离为d,则
,即|2MF|=d.
∴|AM|+2|MF|=|AM|+d.
由于A在椭圆内，过A作AK⊥l,K为垂足，易证|AM|即为|AM|+d的最小值，其值为8-（-2）=10.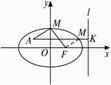 
此时M点纵坐标为
，得横坐标为
.
∴|AM|+2|MF|的最小值为10，这时点M的坐标为（
，
）.
练习册系列答案
相关题目
已知定点A（2，0），圆O的方程为x2+y2=8，动点M在圆O上，那么∠OMA的最大值是（ ）
A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|