题目内容
已知定点A(2,0),圆O的方程为x2+y2=8,动点M在圆O上,那么∠OMA的最大值是( )
A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
分析:设|MA|=x,则可求得|OM|,|AO|的值,进而利用余弦定理得到cos∠OMA的表达式,利用均值不等式求得cos∠OMA的最小值,进而求得∠OMA的最大值.
解答:解:设|MA|=x,则|OM|=2
,|AO|=2
由余弦定理可知cos∠OMA=
=
•(
+x)≥
(当且仅当x=2时等号成立)
∴∠OMA≤
.
故选B.
| 2 |
由余弦定理可知cos∠OMA=
| 8+x2-4 | ||
4
|
| 1 | ||
4
|
| 4 |
| x |
| ||
| 2 |
∴∠OMA≤
| π |
| 4 |
故选B.
点评:本题主要考查了点与圆的位置关系,余弦定理的应用,均值不等式求最值.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
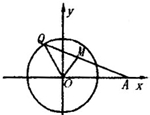 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.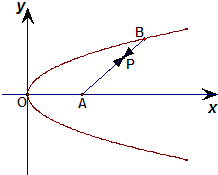 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得