题目内容
设函数f(x)=(x+a)lnx﹣x+a.
(Ⅰ)设g(x)=f'(x),求g(x)函数的单调区间;
(Ⅱ)若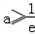 ,试研究函数f(x)=(x+a)lnx﹣x+a的零点个数.
,试研究函数f(x)=(x+a)lnx﹣x+a的零点个数.
(Ⅰ)设g(x)=f'(x),求g(x)函数的单调区间;
(Ⅱ)若
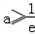 ,试研究函数f(x)=(x+a)lnx﹣x+a的零点个数.
,试研究函数f(x)=(x+a)lnx﹣x+a的零点个数.解:(Ⅰ)g(x)的定义域是(0,+∞)
∵g(x)=f'(x)= +lnx,
+lnx,
∴g'(x)=﹣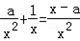 ,
,
(1)当a≤0时,g'(x)>0,
∵g(x)在(0,+∞)上单调递增,故g(x)单调区间是(0,+∞)
(2)当a>0时,g'(x)>0,
∵g(x)在(a,+∞)上单调递增,再由g'(x)<0得g(x)在(0,a)上单调递减.
g(x)的单调区间是(0,a)与(a,+∞)
(Ⅱ)由题(Ⅰ)知,g(x)在x=a时取到最小值,且为g(a)= +lna=1+lna.
+lna=1+lna.
∵a≥ ,
,
∴lna≥﹣1,
∴g(a)≥0。
∴f'(x)≥g(a)≥0.f(x)在(0,+∞)上单调递增,
∵f(e)=(e+a)lne﹣e+a=2a>0,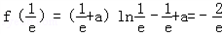 <0,∴
<0,∴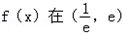 内有零点.
内有零点.
故函数f(x)=(x+a)lnx﹣x+a的零点个数为1.

练习册系列答案
相关题目
 的最小值;
的最小值; 的最小值;
的最小值;