题目内容
 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).(1)求证:AP∥平面EFG;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
分析:(1)由条件可得EF∥CD∥AB,利用直线和平面平行的判定定理证得EF∥平面PAB.同理可证,EG∥平面PAB,
可得平面EFG∥平面PAB.再利用两个平面平行的性质可得AP∥平面EFG.
(2)由条件可得DA、DP、DC互相垂直,故AD⊥平面PCD,AD⊥PC.再由EQ平行且等于
BC可得EQ平行且
等于
AD,故ADEQ为梯形.再根据DE为等腰直角三角形PCD 斜边上的中线,可得DE⊥PC.再利用直线和
平面垂直的判定定理证得PC⊥平面ADQ.
(3)根据VC-EFG=VG-CEF=
•S△CEF•CG=
•(
•EF•DF)•CG,运算求得结果.
可得平面EFG∥平面PAB.再利用两个平面平行的性质可得AP∥平面EFG.
(2)由条件可得DA、DP、DC互相垂直,故AD⊥平面PCD,AD⊥PC.再由EQ平行且等于
| 1 |
| 2 |
等于
| 1 |
| 2 |
平面垂直的判定定理证得PC⊥平面ADQ.
(3)根据VC-EFG=VG-CEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解答: 解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,
解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,
可得EF∥CD∥AB.
由于AB?平面PAB,EF不在平面 PAB内,故有 EF∥平面PAB.
同理可证,EG∥平面PAB.
由于EF、EG是平面EFG内的两条相交直线,
故有平面EFG∥平面PAB.
而PA?平面PAB,∴AP∥平面EFG.
(2)由条件可得,CD⊥AD,CD⊥PD,
而PD、AD是两条相交直线,故CD⊥平面PAD,
∴∠PDA 为二面角PCD-CD-ABCD的平面角.
再由平面PCD⊥平面ABCD,可得PD⊥AD,故DA、DP、DC互相垂直,故AD⊥平面PCD,
而PC?平面PCD,故有AD⊥PC.
∵点Q是线段PB的中点,∴EQ平行且等于
BC,∴EQ平行且等于
AD,故四边形ADEQ为梯形.
再由AD=DC=PD=2,可得DE为等腰直角三角形PCD 斜边上的中线,∴DE⊥PC.
这样,PC垂直于平面ADQ中的两条相交直线AD、DE,∴PC⊥平面ADQ.
(3)VC-EFG=VG-CEF=
•S△CEF•CG=
•(
•EF•DF)•CG=
•(
×1×1)×1=
.
 解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,
解:(1)证明:E、F、G分别为线段PC、PD、BC的中点,可得EF∥CD∥AB.
由于AB?平面PAB,EF不在平面 PAB内,故有 EF∥平面PAB.
同理可证,EG∥平面PAB.
由于EF、EG是平面EFG内的两条相交直线,
故有平面EFG∥平面PAB.
而PA?平面PAB,∴AP∥平面EFG.
(2)由条件可得,CD⊥AD,CD⊥PD,
而PD、AD是两条相交直线,故CD⊥平面PAD,
∴∠PDA 为二面角PCD-CD-ABCD的平面角.
再由平面PCD⊥平面ABCD,可得PD⊥AD,故DA、DP、DC互相垂直,故AD⊥平面PCD,
而PC?平面PCD,故有AD⊥PC.
∵点Q是线段PB的中点,∴EQ平行且等于
| 1 |
| 2 |
| 1 |
| 2 |
再由AD=DC=PD=2,可得DE为等腰直角三角形PCD 斜边上的中线,∴DE⊥PC.
这样,PC垂直于平面ADQ中的两条相交直线AD、DE,∴PC⊥平面ADQ.
(3)VC-EFG=VG-CEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题主要考查直线和平面平行的判定定理、直线和平面垂直的判定定理的应用,用等体积法求棱锥的体积,
属于中档题.
属于中档题.

练习册系列答案
相关题目
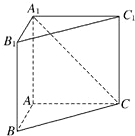 如图所示,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图所示,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=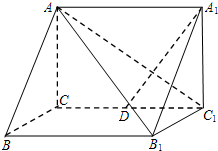 (2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
(2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,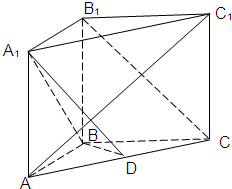 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点. 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.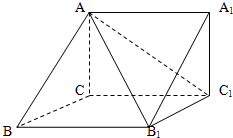 (2011•重庆模拟)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=
(2011•重庆模拟)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=