题目内容
已知P为空间中任意一点,A、B、C、D四点满足任意三点均不共线,但四点共面,且
=
-x
+
,则实数x的值为( )
| PA |
| 4 |
| 3 |
| PB |
| PC |
| 1 |
| 6 |
| DB |
分析:利用空间向量基本定理,及向量共面的条件,即可得到结论.
解答:解:
=
-x
+
=
-x
+
(
-
)=
-x
-
,
又∵P是空间任意一点,A、B、C、D四点满足任三点均不共线,但四点共面,
∴
-x-
=1,
解得 x=
,
故选A.
| PA |
| 4 |
| 3 |
| PB |
| PC |
| 1 |
| 6 |
| DB |
| 4 |
| 3 |
| PB |
| PC |
| 1 |
| 6 |
| PB |
| PD |
| 3 |
| 2 |
| PB |
| PC |
| 1 |
| 6 |
| PD |
又∵P是空间任意一点,A、B、C、D四点满足任三点均不共线,但四点共面,
∴
| 3 |
| 2 |
| 1 |
| 6 |
解得 x=
| 1 |
| 3 |
故选A.
点评:本题考查空间向量基本定理,考查向量共面的条件,属于中档题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
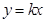 与圆
与圆 恒有公共点;
恒有公共点;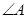 为△ABC的内角,则
为△ABC的内角,则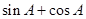 最小值为
最小值为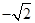 ;
; }中,
}中,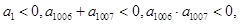 则使其前n项和
则使其前n项和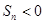 成立的最大正整数为2013;
成立的最大正整数为2013; 与圆
与圆 恒有公共点;
恒有公共点; 为△ABC的内角,则
为△ABC的内角,则 最小值为
最小值为 ;
; }中,
}中, 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;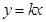 与圆
与圆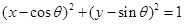 恒有公共点;
恒有公共点;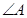 为△ABC的内角,则
为△ABC的内角,则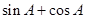 最小值为
最小值为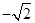 ;
;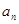 }中,
}中,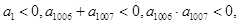 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;