题目内容
若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1、x2总有以下不等式(1)证明定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(2)对于(1)中的二次函数f(x)=ax2+bx+c(a<0),若|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,求|f(4)|取得最大值时函数y=f(x)的解析式.
思路解析:本题是阅读理解题目,根据题意对凸函数的定义进行变形证明,在求函数解析式是要想办法用f(1)、f(2)和f(3)表示f(4),从而求出f(4)的最大值,这样把不等关系转化为相等关系求出待定系数.
证明:(1)任取x1,x2∈R,则
2f(![]() )-[f(x1)+f(x2)]
)-[f(x1)+f(x2)]
=2[a(![]() )2+b
)2+b![]() +c]-[ax12+bx1+c]-[ax22+bx2+c]
+c]-[ax12+bx1+c]-[ax22+bx2+c]
=![]() [(x1+x2)2-2(x12+x22)]=-
[(x1+x2)2-2(x12+x22)]=-![]() (x1-x2)2.
(x1-x2)2.
∵a<0,
∴2f(![]() )-[f(x1)+f(x2)]≥0.
)-[f(x1)+f(x2)]≥0.
∴![]() [f(x1)+f(x2)]≤f(
[f(x1)+f(x2)]≤f(![]() ).
).
∴由定义得y=f(x)是R上的凸函数.
(2)∵
又∵|f(4)|=|16a+4b+c|=|f(1)-3f(2)+3f(3)|≤|f(1)|+3|f(2)|+3|f(3)|.
又∵|f(1)|≤1,|f(2)|≤2,|f(3)|≤3.
∴|f(4)|≤|f(1)|+3|f(2)|+3|f(3)|≤16.
∴当且仅当 时取等号,代入上式得
时取等号,代入上式得
∴f(x)=-4x2+15x-12.

练习册系列答案
相关题目

 的单调性;
的单调性;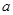 的取值范围;
的取值范围;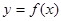 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式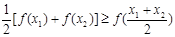 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数 ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.