Question

（1）一家保险公司调查其总公司营业部的加班程度，收集了10周中每周加班工作时间y（小时）与签发新保单数目x的数据如下表，则用最小二乘估计求出的回归直线方程是 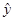   =0.1181+0.003585x            .

x	825	215	1070	550	480	920	1350	325	670	1215
y	3.5	1.0	4.0	2.0	1.0	3.0	4.5	1.5	3.0	5.0

（2）上题中，每周加班时间y与签发新保单数目x之间的相关系数    ，查表得到的相关系数临界值r_0.05=          ，这说明题中求得的两变量之间的回归直线方程是          （有／无）意义的．

（3）上面题中，若该公司预计下周签发新保单1000张，需要的加班时间的估计是           .

 

Answer 1

【答案】

（1）b=0.003585，a=0.1181. （2）r=0.9489、0.632 、有

（3）x₀=1000，=0.1181＋0.003585x₀=3.7（小时）．

【解析】

试题分析：（1）由公式计算得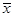：=762，l_xx=1297860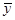，=2.85，l_xy=4653，

∴ b=0.003585，a=0.1181.

（2）r=0.9489、0.632 、有

（3）计算得x₀=1000，=0.1181＋0.003585x₀=3.7（小时）．

考点：本题主要考查回归直线方程及计算能力．

点评：这是一道实际应用问题，解题的关键是明确线性回归直线一定过样本中心点，把样本中心点代入求出b的值，注意数字的运算。