题目内容
一家保险公司调查其总公司营业部的加班程度，收集了10周中每周加班工作时间y（h）与签发新保单数目x的数据如下表：x | 825 | 215 | 1070 | 550 | 480 | 920 | 1350 | 325 | 670 | 1215 |
y | 3.5 | 1.0 | 4.0 | 2.0 | 1.0 | 3.0 | 4.5 | 1.5 | 3.0 | 5.0 |
则y与x的线性回归方程是______________.（保留四位有效数字）
=0.1181+0.003585x
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
一家保险公司调查其总公司营业部的加班程度,收集了10周中每周加班工作时间y(小时)与签发新保单数目x的数据如下表,则用最小二乘估计求出的回归直线方程是___________.
x | 825 | 215 | 1 070 | 550 | 480 | 920 | 1 350 | 325 | 670 | 1 215 |
y | 3.5 | 1.0 | 4.0 | 2.0 | 1.0 | 3.0 | 4.5 | 1.5 | 3.0 | 5.0 |
（1）一家保险公司调查其总公司营业部的加班程度，收集了10周中每周加班工作时间y（小时）与签发新保单数目x的数据如下表，则用最小二乘估计求出的回归直线方程是
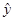=0.1181+0.003585x
.
|
x |
825 |
215 |
1070 |
550 |
480 |
920 |
1350 |
325 |
670 |
1215 |
|
y |
3.5 |
1.0 |
4.0 |
2.0 |
1.0 |
3.0 |
4.5 |
1.5 |
3.0 |
5.0 |
（2）上题中，每周加班时间y与签发新保单数目x之间的相关系数 ，查表得到的相关系数临界值r0.05= ，这说明题中求得的两变量之间的回归直线方程是 （有／无）意义的．
（3）上面题中，若该公司预计下周签发新保单1000张，需要的加班时间的估计是 .