题目内容
【题目】已知![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) 函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;(2)
上单调递减;(2) ![]() .
.
【解析】试题分析:
(1)求出导数![]() ,在定义域内,解不等式
,在定义域内,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)题设不等式可变形为
得减区间;(2)题设不等式可变形为![]() ,分别设
,分别设![]() ,
, ![]() ,求出它们的导数
,求出它们的导数![]() ,通过解相应不等式得出单调区间,求出最值,恰好是
,通过解相应不等式得出单调区间,求出最值,恰好是![]() 时,
时, ![]() 取最小值,
取最小值, ![]() 最最大值,因此要使原不等式恒成立,只要
最最大值,因此要使原不等式恒成立,只要![]() 即可.
即可.
试题解析:
(1)由![]() 得:
得: 
由于定义域为![]() ,
,
所以由![]() 得:
得: ![]()
所以由![]() 得:
得: ![]()
即得函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减。
上单调递减。
(2)由不等式![]() 恒成立,
恒成立,
即![]() 恒成立
恒成立
设![]() 得:
得:
![]()
因为它们的定义域![]() ,所以易得:
,所以易得:
函数![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增;
上单调递增;
函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
这两个函数在![]() 处,
处, ![]() 有最小值,
有最小值, ![]() 有最大值,
有最大值,
所以要使不等式![]() 恒成立,
恒成立,
则只需满足![]() ,即
,即![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
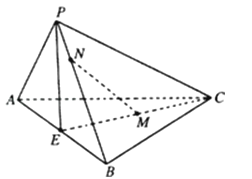
【题目】如图,在三棱锥P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
(Ⅰ)证明:平面PCE⊥平面PAB;
(Ⅱ)证明:MN∥平面PAC.