题目内容
已知椭圆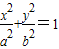 的左、右焦点分别为F1,F2,过点F1作直线与椭圆相交,被椭圆截得的最短的线段
的左、右焦点分别为F1,F2,过点F1作直线与椭圆相交,被椭圆截得的最短的线段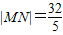 ,且△MF2N的周长为20,则椭圆的离心率e等于 .
,且△MF2N的周长为20,则椭圆的离心率e等于 .
【答案】分析:椭圆的离心率e=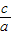 ,根据题目条件,MN的长度为椭圆通径的长,△MF2N的周长为4a,列方程即可解得a、c的值,进而求得离心率.
,根据题目条件,MN的长度为椭圆通径的长,△MF2N的周长为4a,列方程即可解得a、c的值,进而求得离心率.
解答:解:解:∵△MF2N的周长=MF1+MF2+NF1+NF2=2a+2a=4a=20,∴a=5,
又由椭圆的几何性质,过焦点的最短弦为通径长 ,
,
∴MN=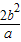 =
=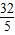 ,
,
∴b2=16,c2=a2-b2=9,
∴c=3
∴e=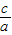 =
= ,
,
故答案为: .
.
点评:本题主要考查了椭圆的定义,椭圆的几何性质,此类型题目要求我们应掌握椭圆中特殊的线段的长度,如通径等.
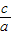 ,根据题目条件,MN的长度为椭圆通径的长,△MF2N的周长为4a,列方程即可解得a、c的值,进而求得离心率.
,根据题目条件,MN的长度为椭圆通径的长,△MF2N的周长为4a,列方程即可解得a、c的值,进而求得离心率.解答:解:解:∵△MF2N的周长=MF1+MF2+NF1+NF2=2a+2a=4a=20,∴a=5,
又由椭圆的几何性质,过焦点的最短弦为通径长
 ,
,∴MN=
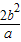 =
=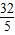 ,
,∴b2=16,c2=a2-b2=9,
∴c=3
∴e=
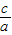 =
= ,
,故答案为:
 .
.点评:本题主要考查了椭圆的定义,椭圆的几何性质,此类型题目要求我们应掌握椭圆中特殊的线段的长度,如通径等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线