题目内容
已知函数f(x)=x3-2ax2+x(1)若函数f(x)在(1,+∞)上为增函数,求实数a的最大值;
(2)当x∈(0,+∞)时,f(x)≥ax恒成立,求a的取值范围.
【答案】分析:(1)由函数f(x)在(1,+∞)上为增函数,得f′(x)≥0(x>1)恒成立,进而可转化为函数最值问题解决.
(2)f(x)≥ax即x3-2ax2+x≥ax(x>0)恒成立,可变为a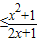 (x>0)恒成立,只需y求出
(x>0)恒成立,只需y求出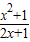 在(0,+∞)上的最小值即可.
在(0,+∞)上的最小值即可.
解答:解:(1)f′(x)=3x2-4ax+1,
∵f(x)在(1,+∞)上为增函数,
∴f′(x)=3x2-4ax+1≥0(x>1)恒成立,即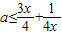 (x>1)恒成立.
(x>1)恒成立.
令h(x)=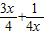 ,得
,得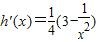
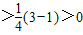 (x>1),
(x>1),
∴h(x)在(1,+∞)上单调递增,h(x)>h(1)=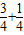 =1,
=1,
∴a≤1,故实数a的最大值为1.
(Ⅱ)由题意知x3-2ax2+x≥ax(x>0)恒成立,即a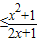 (x>0)恒成立,
(x>0)恒成立,
令r(x)=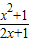 (x>0),则
(x>0),则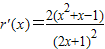 ,由r′(x)<0得0<x
,由r′(x)<0得0<x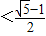 ;由r′(x)>0得x
;由r′(x)>0得x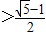 ,
,
∴r(x)在(0,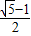 )上单调递减,在
)上单调递减,在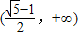 上单调递增,∴
上单调递增,∴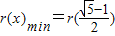 =
=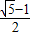 .
.
∴a≤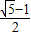 ,
,
故a的取值范围为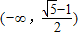 .
.
点评:本题考查了利用导数研究函数的单调性、最值问题,对于恒成立问题常转化为最值问题或分离参数后再求最值.
(2)f(x)≥ax即x3-2ax2+x≥ax(x>0)恒成立,可变为a
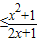 (x>0)恒成立,只需y求出
(x>0)恒成立,只需y求出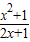 在(0,+∞)上的最小值即可.
在(0,+∞)上的最小值即可.解答:解:(1)f′(x)=3x2-4ax+1,
∵f(x)在(1,+∞)上为增函数,
∴f′(x)=3x2-4ax+1≥0(x>1)恒成立,即
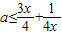 (x>1)恒成立.
(x>1)恒成立.令h(x)=
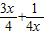 ,得
,得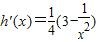
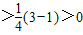 (x>1),
(x>1),∴h(x)在(1,+∞)上单调递增,h(x)>h(1)=
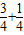 =1,
=1,∴a≤1,故实数a的最大值为1.
(Ⅱ)由题意知x3-2ax2+x≥ax(x>0)恒成立,即a
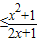 (x>0)恒成立,
(x>0)恒成立,令r(x)=
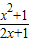 (x>0),则
(x>0),则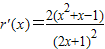 ,由r′(x)<0得0<x
,由r′(x)<0得0<x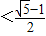 ;由r′(x)>0得x
;由r′(x)>0得x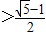 ,
,∴r(x)在(0,
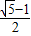 )上单调递减,在
)上单调递减,在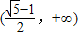 上单调递增,∴
上单调递增,∴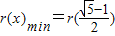 =
=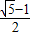 .
.∴a≤
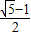 ,
,故a的取值范围为
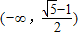 .
.点评:本题考查了利用导数研究函数的单调性、最值问题,对于恒成立问题常转化为最值问题或分离参数后再求最值.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|