题目内容

选做题（1）设x是正数，求证：(1+x)(1+x2)(1+x3)≥8x3；

（2）若x∈R，不等式(1+x)(1+x2)(1+x3)≥8x3是否仍然成立？如果仍成立，请给出证明；如果不成立，请举出一个使它不成立的x的值.

简证：(1)∵x＞0，∴1+x≥2＞0，1+x2≥2x＞0，1+x3≥2x＞0，三个同向正值不等式相乘得(1+x)(1+x2)(1+x3)≥8x3.

简解：(2)x∈R时原不等式仍然成立.

思路1：分类讨论x=0、-1＜x＜0、x=-1、x＜-1证明；

思路2：左边=(1+x)2(1+x2)［(x)2+］≥0.

练习册系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
A．[选修4-1：几何证明选讲]
已知△ABC中，AB=AC，D是△ABC外接圆劣弧AC上的点（不与点A，C重合），延长BD至点E．
求证：AD的延长线平分∠CDE
B．[选修4-2：矩阵与变换]
已知矩阵A=
12
-14

（1）求A的逆矩阵A-1；
（2）求A的特征值和特征向量．
C．[选修4-4：坐标系与参数方程]
已知曲线C的极坐标方程为ρ=4sinθ，以极点为原点，极轴为x轴的非负半轴建立平面直角坐标系，直线l的参数方程为
x=
1
2
t
y=
3
2
t+1
（t为参数），求直线l被曲线C截得的线段长度．
D．[选修4-5，不等式选讲]（本小题满分10分）
设a，b，c均为正实数，求证：
1
2a
+
1
2b
+
1
2c
≥
1
b+c
+
1
c+a
+
1
a+b
．
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答题纸指定区域内 作答．解答应写出文字说明、证明过程或演算步骤．
A．如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．
B．已知二阶矩阵A=
2a
b0
属于特征值-1的一个特征向量为
1
-3
，求矩阵A的逆矩阵．

C．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，曲线C的极坐标方程ρ2cos2θ+3ρ2sin2θ=3，直线l的参数方程为
x=-
3
t
y=1+t
（t为参数，t∈{R}）．试求曲线C上点M到直线l的距离的最大值．
D．（1）设x是正数，求证：（1+x）（1+x2）（1+x3）≥8x3；
（2）若x∈R，不等式（1+x）（1+x2）（1+x3）≥8x3是否仍然成立？如果仍成立，请给出证明；如果不成立，请举出一个使它不成立的x的值．
【选做题】在A，B，C，D四小题中只能选做2题，每题10分，共计20分．请在答题卡指定区域内作答，解答时写出文字说明、证明过程或演算步骤．
21-1．（选修4-2：矩阵与变换）
设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
（1）求矩阵M的特征值及相应的特征向量；
（2）求逆矩阵M-1以及椭圆
x2
4
+
y2
9
=1在M-1的作用下的新曲线的方程．
21-2．（选修4-4：参数方程）
以直角坐标系的原点O为极点，x轴的正半轴为极轴．已知点P的直角坐标为（1，-5），点M的极坐标为（4，
π
2
），若直线l过点P，且倾斜角为 
π
3
，圆C以M为圆心、4为半径．
（1）求直线l关于t的参数方程和圆C的极坐标方程；
（2）试判定直线l和圆C的位置关系．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）
A．设函数f（x）=|2x+1|-|x-4|．则不等式f（x）＞2的解集为
{x|x＜-7或x＞
5
3
}
{x|x＜-7或x＞
5
3
}
；
B．（坐标系与参数方程选做题）曲线C：
x=-2+2cosα
y=2sinα
（α为参数），若以点O（0，0）为极点，x正半轴为极轴建立极坐标系，则该曲线的极坐标方程是
ρ=-4cosθ
ρ=-4cosθ
．

C．（几何证明选讲选做题） 如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，弧AE=弧AC，DE交AB于F，且AB=2BP=4，则PF=
3
3
．
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答题纸指定区域内 作答．解答应写出文字说明、证明过程或演算步骤．
A．如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．
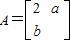B．已知二阶矩阵属于特征值-1的一个特征向量为，求矩阵A的逆矩阵．

C．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，曲线C的极坐标方程ρ2cos2θ+3ρ2sin2θ=3，直线l的参数方程为（t为参数，t∈{R}）．试求曲线C上点M到直线l的距离的最大值．
D．（1）设x是正数，求证：（1+x）（1+x2）（1+x3）≥8x3；
（2）若x∈R，不等式（1+x）（1+x2）（1+x3）≥8x3是否仍然成立？如果仍成立，请给出证明；如果不成立，请举出一个使它不成立的x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网