题目内容
求函数f(x)=ln(1+x)- x2在[0,2]上的最大值和最小值。
x2在[0,2]上的最大值和最小值。
 x2在[0,2]上的最大值和最小值。
x2在[0,2]上的最大值和最小值。 解:f′(x)= ,令
,令 ,化简得x2+x- 2=0,
,化简得x2+x- 2=0,
解得x1=-2(舍去),x2=1,
当0≤x<1时,f′(x)>0, f(x)单调递增;
当1<x≤2时,f′(x)<0,f(x)单调递减,
所以 为函数f(x)的最大值,
为函数f(x)的最大值,
又因为f(0)=0,f(2)=ln3-1>0,f(1)>f(2),
所以f(0)=0为函数f(x)在[0,2]上的最小值,f(1)= 为函数f(x)在[0,2] 上的最大值。
为函数f(x)在[0,2] 上的最大值。
 ,令
,令 ,化简得x2+x- 2=0,
,化简得x2+x- 2=0,解得x1=-2(舍去),x2=1,
当0≤x<1时,f′(x)>0, f(x)单调递增;
当1<x≤2时,f′(x)<0,f(x)单调递减,
所以
 为函数f(x)的最大值,
为函数f(x)的最大值,又因为f(0)=0,f(2)=ln3-1>0,f(1)>f(2),
所以f(0)=0为函数f(x)在[0,2]上的最小值,f(1)=
 为函数f(x)在[0,2] 上的最大值。
为函数f(x)在[0,2] 上的最大值。 
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 -ln(x+a)(x∈(0,+∞))的单调区间。
-ln(x+a)(x∈(0,+∞))的单调区间。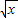 -ln(x+a)(x∈(0,+∞))的单调区间.
-ln(x+a)(x∈(0,+∞))的单调区间. -ln(x+a)(x∈(0,+∞))的单调区间.
-ln(x+a)(x∈(0,+∞))的单调区间.