题目内容
18.求函数f(x)=ln(1+x)-
18.本小题主要考查函数的导数计算,利用导数讨论函数的性质,判断函数的最大值、最小值以及综合运算能力.
解:f′(x)=![]() -
-![]() x,
x,
令![]() -
-![]() x=0,
x=0,
化简为 x2+x-2=0,
解得 x1=-2(舍去),x2=1.
当0≤x<1时,f′(x)>0,f(x)单调递增;
当1<x≤2时,f′(x)<0,f(x)单调递减.
所以f(1)=ln2-![]() 为函数f(x)的极大值.
为函数f(x)的极大值.
又因为f(0)=0,f(2)=ln3-1>0,f(1)>f(2),
所以f(0)=0为函数f(x)在[0,2]上的最小值,
f(1)=ln2-![]() 为函数f(x)在[0,2]上的最大值.
为函数f(x)在[0,2]上的最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -ln(x+a)(x∈(0,+∞))的单调区间。
-ln(x+a)(x∈(0,+∞))的单调区间。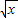 -ln(x+a)(x∈(0,+∞))的单调区间.
-ln(x+a)(x∈(0,+∞))的单调区间. -ln(x+a)(x∈(0,+∞))的单调区间.
-ln(x+a)(x∈(0,+∞))的单调区间.