题目内容
(2013•青岛二模)已知两条直线y=ax-2和3x-(a+2)y+1=0互相垂直,则a等于
-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:把直线方程都化为一般式,然后利用A1x+B1y+C1=0和A2x+B2y+C2=0垂直的充要条件是A1A2+B1B2=0列式求解a的值.
解答:解:由y=ax-2,得ax-y-2=0,
又3x-(a+2)y+1=0,
不妨设A1=a,B1=-1,A2=3,B2=-(a+2),
∵两条直线y=ax-2和3x-(a+2)y+1=0互相垂直,
∴A1A2+B1B2=0,即3a+(-1)×[-(a+2)]=0,解得:a=-
.
∴使两条直线y=ax-2和3x-(a+2)y+1=0互相垂直的a的值为-
.
故答案为:-
.
又3x-(a+2)y+1=0,
不妨设A1=a,B1=-1,A2=3,B2=-(a+2),
∵两条直线y=ax-2和3x-(a+2)y+1=0互相垂直,
∴A1A2+B1B2=0,即3a+(-1)×[-(a+2)]=0,解得:a=-
| 1 |
| 2 |
∴使两条直线y=ax-2和3x-(a+2)y+1=0互相垂直的a的值为-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了直线的一般式方程和直线垂直的关系,考查了A1x+B1y+C1=0和A2x+B2y+C2=0垂直的充要条件,是基础题.

练习册系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=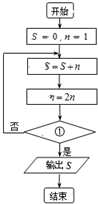 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )