题目内容
与x2-y2=0无公共点,且以3x±2y=0为渐近线的双曲线的离心率为
- A.

- B.
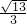
- C.
 或
或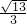
- D.以上都不正确
B
分析:由双曲线的渐近线方程是3x±2y=0,可知渐近线的斜率为 ,与x2-y2=0无公共点,焦点在y轴,由此可以求出该双曲线的离心率.
,与x2-y2=0无公共点,焦点在y轴,由此可以求出该双曲线的离心率.
解答:∵双曲线的渐近线方程是3x±2y=0,可知渐近线的斜率为 ,
,
与x2-y2=0无公共点,焦点在y轴,所以 ,即
,即
可得 ,解得e=
,解得e=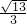 .
.
故选B.
点评:本题考查双曲线的渐近线和离心率,解题的关键是判断双曲线的焦点所在的轴,以及由渐近线方程导出a,b,c的关系.
分析:由双曲线的渐近线方程是3x±2y=0,可知渐近线的斜率为
 ,与x2-y2=0无公共点,焦点在y轴,由此可以求出该双曲线的离心率.
,与x2-y2=0无公共点,焦点在y轴,由此可以求出该双曲线的离心率.解答:∵双曲线的渐近线方程是3x±2y=0,可知渐近线的斜率为
 ,
,与x2-y2=0无公共点,焦点在y轴,所以
 ,即
,即
可得
 ,解得e=
,解得e=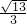 .
.故选B.
点评:本题考查双曲线的渐近线和离心率,解题的关键是判断双曲线的焦点所在的轴,以及由渐近线方程导出a,b,c的关系.

练习册系列答案
相关题目