题目内容
已知fn(x)=a1x+a2x2+…+anxn,fn(-1)=(-1)n·n，n=1,2,3,….（1）求a1、a2、a3；
（2）求数列{an}的通项公式；
（3）求证：fn(
)＜1.
（1）解：由已知f1(-1)=-a1=-1,∴a1=1.
f2(-1)=-a1+a2=2,∴a2=3.
f3(-1)=-a1+a2-a3=-3,∴a3=5.
（2）解:∵(-1)n+1·an+1=fn+1(-1)-fn(-1)=(-1)n+1·(n+1)-(-1)n·n,
∴an+1=(n+1)+n,即an+1=2n+1.∴对于任意的n=1,2,3,…,an=2n-1.
（3）证明:fn(x)=x+3x2+5x3+…+(2n-1)xn,
∴fn()=
+3(
)2+5(
)3+…+(2n-1)(
)n.①
·fn(
)=(
)2+3(
)3+5(
)4+…+(2n-1)(
)n+1.②
①-②,得
fn(
)=
+2(
)2+2(
)3+…+2(
)n-(2n-1)(
)n+1
=
+
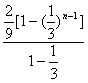-(2n-1)(
)n+1=
(
)n.∴fn(
)=1
.
又n=1,2,3,…,故fn(
)＜1.
练习册系列答案
阅读快车系列答案
相关题目
)＜1.