题目内容
已知双曲线两顶点间距离为
解析:如图
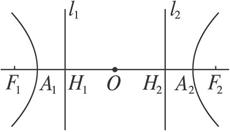
图
由离心率定义![]() ,
,
∴A1H1=![]() A
A
又A
∴A1H1=![]() .
.
∴OH1=OA1-A1H1
=a-![]() =
=![]() .
.
由对称性,得OH2=![]() .
.
∴H1H2=![]() .
.
答案: ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知双曲线两顶点间距离为
解析:如图

图
由离心率定义![]() ,
,
∴A1H1=![]() A
A
又A
∴A1H1=![]() .
.
∴OH1=OA1-A1H1
=a-![]() =
=![]() .
.
由对称性,得OH2=![]() .
.
∴H1H2=![]() .
.
答案: ![]()

 阅读快车系列答案
阅读快车系列答案