题目内容
 ,α、β
,α、β 等于
等于
- A.

- B.

- C.

- D.

B
分析:由根与系数的关系求出tanα,tanβ的和与积,再由正切的两角和公式计算出tan(α+β)值,再由同角三角函数的基本关系求出两角和的余弦值.
解答:由题设条件tanα+tanβ=-3 ,tanα×tanβ=4
,tanα×tanβ=4
tan(α+β)= =
= =
=
又α、β∈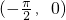 ,则α+β∈(-π,0)
,则α+β∈(-π,0)
∴α+β∈(-π,- )
)
取α+β终边上一点P(-1,- )
)
则OP=2,cos(α+β)=-
故就选B.
点评:本题考查一元二次方程的根与系数的关系及两角和的正切公式、同角三角函数的关系,知识覆盖面广,技巧性强.
分析:由根与系数的关系求出tanα,tanβ的和与积,再由正切的两角和公式计算出tan(α+β)值,再由同角三角函数的基本关系求出两角和的余弦值.
解答:由题设条件tanα+tanβ=-3
 ,tanα×tanβ=4
,tanα×tanβ=4tan(α+β)=
 =
= =
=
又α、β∈
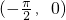 ,则α+β∈(-π,0)
,则α+β∈(-π,0)∴α+β∈(-π,-
 )
)取α+β终边上一点P(-1,-
 )
)则OP=2,cos(α+β)=-

故就选B.
点评:本题考查一元二次方程的根与系数的关系及两角和的正切公式、同角三角函数的关系,知识覆盖面广,技巧性强.

练习册系列答案
相关题目
 的公比
的公比 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 外接圆的半径为1,圆心为O.且
外接圆的半径为1,圆心为O.且 ,则
,则 等于( )
等于( ) (B)
(B) (C)
(C) (D)3
(D)3 为虚数单位,则
为虚数单位,则 的实部与虚部的乘积等于( )
的实部与虚部的乘积等于( )  B.
B.
 C.
C.
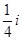 D.
D.
