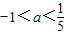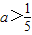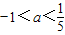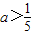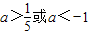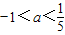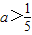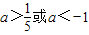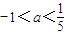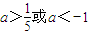题目内容
若f(x)=3ax+1-2a在(-1,1)上存在零点,则实数a的取值范围是
- A.
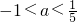
- B.
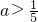
- C.

- D.a<-1
C
分析:根据零点的性质和不等式性质进行求解.
解答:由f(x)=3ax+1-2a=0得 ,
,
∵f(x)=3ax+1-2a在(-1,1)上存在零点,
∴ ,解得
,解得 .
.
故选C.
点评:求出零点后再根据零点的范围判断实数a的取值范围.
分析:根据零点的性质和不等式性质进行求解.
解答:由f(x)=3ax+1-2a=0得
 ,
,∵f(x)=3ax+1-2a在(-1,1)上存在零点,
∴
 ,解得
,解得 .
.故选C.
点评:求出零点后再根据零点的范围判断实数a的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若f(x)=3ax+1-2a在(-1,1)上存在零点,则实数a的取值范围是( )
A、-1<a<
| ||
B、a>
| ||
C、a>
| ||
| D、a<-1 |