题目内容
如图△ABC为正三角形，边长为2，以点A为圆心，1为半径作圆．（1）若
| CD |
| 1 |
| 3 |
| DB |
| AD |
（2）PQ为圆A的任意一条直径，求
| BP |
| CQ |
分析：（1）先将向量
用向量
与
线性表示，然后根据|
| =
进行求解；
（2）
•
可转化成
•
= (
+
)(
+
)，然后展开化简，可得
•
=1+
•
=1+2cosθ（其中θ为
与
的夹角），最后根据三角形函数求出最值．
| AD |
| AC |
| CB |
| a |
|
（2）
| BP |
| CQ |
| BP |
| CQ |
| BA |
| AP |
| CA |
| AQ |
| BP |
| CQ |
| AQ |
| BC |
| AQ |
| BC |
解答：解：（1）∵
=
，
∴
=
+
∴|
|=
=
=
；
（2）
•
= (
+
)(
+
)
=1+
(
-
)
=1+
•
=1+2cosθ（其中θ为
与
的夹角）
所以θ=0时，
•
的最大值为3．
| CD |
| 1 |
| 3 |
| DB |
∴
| AD |
| AC |
| 1 |
| 4 |
| CB |
∴|
| AD |
(
|
|
| ||
| 2 |
（2）
| BP |
| CQ |
| BA |
| AP |
| CA |
| AQ |
=1+
| AQ |
| BA |
| CA |
=1+
| AQ |
| BC |
=1+2cosθ（其中θ为
| AQ |
| BC |
所以θ=0时，
| BP |
| CQ |
点评：本题主要考查了向量在几何中的应用，以及向量的模和向量的基本运算，同时考查了转化的思想，属于中档题．
练习册系列答案
相关题目
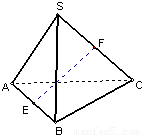
如图，S是边长为a的正三角ABC所在平面外一点，SA=SB=SC=a，E、F是AB和SC的中点，则异面直线SA与EF所成的角为
，延长CB到D，使CB＝BD．
