题目内容
(本小题满分18分)已知函数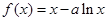 ,
,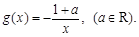
(Ⅰ)若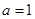 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数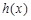 的单调区间;
的单调区间;
(Ⅲ)若在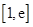 (
(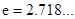 )上存在一点
)上存在一点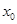 ,使得
,使得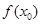
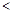
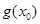 成立,求
成立,求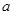 的取值范围.
的取值范围.
【答案】
(Ⅰ) 在
在 处取得极小值1;(Ⅱ)
处取得极小值1;(Ⅱ) 时,
时, 在
在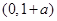 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;  时,函数
时,函数 在
在 上单调递增。
上单调递增。
(Ⅲ)  或
或 .
.
【解析】
试题分析:(Ⅰ)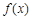 的定义域为
的定义域为 ,
,
当 时,
时, ,
,
|
|
|
1 |
|
|
|
— |
0 |
+ |
|
|
|
极小 |
|
所以 在
在 处取得极小值1.
处取得极小值1.
(Ⅱ) ,
,
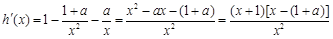
①当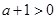 时,即
时,即 时,在
时,在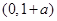 上
上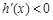 ,在
,在 上
上 ,
,
所以 在
在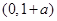 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;
②当 ,即
,即 时,在
时,在 上
上 ,
,
所以函数 在
在 上单调递增.
上单调递增.
(III)在 上存在一点
上存在一点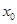 ,使得
,使得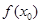

 成立,即 在
成立,即 在 上存在一点
上存在一点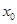 ,使得
,使得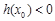 ,
,
即函数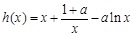 在
在 上的最小值小于零.
上的最小值小于零.
由(Ⅱ)可知
①当 ,即
,即 时,
时, 在
在 上单调递减,
上单调递减,
所以 的最小值为
的最小值为 ,由
,由 可得
可得 ,
,
因为 ,所以
,所以 ;
;
②当 ,即
,即 时,
时,  在
在 上单调递增,
上单调递增,
所以 的最小值为
的最小值为 ,由
,由 可得
可得 ;
;
③当 ,即
,即 时, 可得
时, 可得 的最小值为
的最小值为 ,
,
因为 ,所以
,所以
故
此时, 不成立.
不成立.
综上讨论可得所求 的取值范围是:
的取值范围是: 或
或 .
.
考点:利用导数研究函数的单调性;利用导数研究函数的极值。
点评:①极值点的导数为0,但导数为0的点不定是极值点。②利用导数研究函数的单调性时,一定要先求函数的定义域。③注意恒成立问题与存在性问题的区别。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目




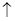
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成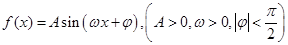 的图象的一部分如下图所示。
的图象的一部分如下图所示。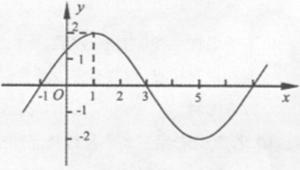
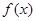 的解析式;
的解析式;
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围;