题目内容
5.若正方形ABCD的边长为1,则$\overrightarrow{BD}$•$\overrightarrow{BC}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 直接利用向量的数量积求解即可.
解答 解:正方形ABCD的边长为1,则$\overrightarrow{BD}$•$\overrightarrow{BC}$=|$\overrightarrow{BD}$|•|$\overrightarrow{BC}$|cos<$\overrightarrow{BD}$,$\overrightarrow{BC}$>=$\sqrt{2}×1×\frac{\sqrt{2}}{2}$=1.
故选:B.
点评 本题考查平面向量的数量积的求法,考查计算能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
16.命题“?x∈R,f(x)g(x)≠0”的否定是( )
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
17.某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中,最大的侧面的面积为( )
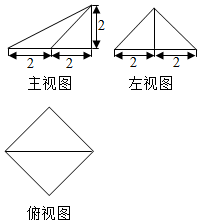

| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
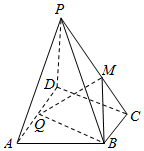 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.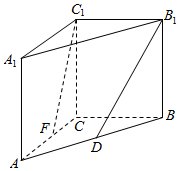 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
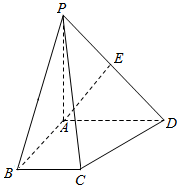 四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.
四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.