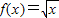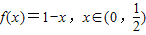题目内容
我们把具有以下性质的函数f(x)称为“好函数”:对于在f(x)定义域内的任意三个数a,b,c,若这三个数能作为三角形的三边长,则f(a),f(b),f(c)也能作为三角形的三边
长.现有如下一些函数:
①
②
③f(x)=ex,x∈(0,1)
④f(x)=sinx,x∈(0,π).
其中是“好函数”的序号有
- A.①②
- B.①②③
- C.②③④
- D.①③④
B
分析:根据“好函数”的定义,可以证出①②③的函数都满足条件,是“好函数”;而④可以通过举出反例,得到它不满足条件,故不是“好函数”.由此得到本题的答案.
解答:①设a、b、c∈(0,+∞)且a+b>c
则( +
+ )2=a+b+2
)2=a+b+2 >c,可得
>c,可得 +
+ >
> ,
,
同理有 +
+ >
> ,
, +
+ >
> ,所以
,所以 是“好函数”;
是“好函数”;
②设a、b、c∈(0, )且a+b>c
)且a+b>c
则(1-a)+(1-b)>1>1-c,同理可得(1-b)+(1-c)>1-a,(1-c)+(1-a)>1-b,
所以 是“好函数”;
是“好函数”;
③设a、b、c∈(0,1)且a+b>c
(i)若a≤ln2且b≤ln2,则ea+eb≥2
∵ln2≥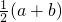 ,∴2≥
,∴2≥ 即2≥
即2≥
由此可得ea+eb≥
 =ea+b>ec
=ea+b>ec
(ii)若a、b中至少有一个大于ln2,不妨设a>ln2
则ea+eb>eln2+e0=2+1=3,而ec<e1<3
∴ea+eb>ec,
综上所述,得ea+eb>ec,同理可得eb+ec>ea,ec+ea>eb.
因此f(x)=ex,x∈(0,1),是“好函数”;
④设a、b、c∈(0,π),取a= ,b=
,b= ,c=
,c=
得sina=sinb= ,sinc=1.虽然a+b>c,但是sina+sinb=sinc,
,sinc=1.虽然a+b>c,但是sina+sinb=sinc,
不满足“好函数”的定义,故f(x)=sinx,x∈(0,π),不是“好函数”.
故选:B
点评:本题给出“好函数”的定义,要我们找出满足条件的函数.着重考查了基本初等函数的性质、不等式的证明和简单的演绎推理等知识,属于中档题.
分析:根据“好函数”的定义,可以证出①②③的函数都满足条件,是“好函数”;而④可以通过举出反例,得到它不满足条件,故不是“好函数”.由此得到本题的答案.
解答:①设a、b、c∈(0,+∞)且a+b>c
则(
 +
+ )2=a+b+2
)2=a+b+2 >c,可得
>c,可得 +
+ >
> ,
,同理有
 +
+ >
> ,
, +
+ >
> ,所以
,所以 是“好函数”;
是“好函数”;②设a、b、c∈(0,
 )且a+b>c
)且a+b>c则(1-a)+(1-b)>1>1-c,同理可得(1-b)+(1-c)>1-a,(1-c)+(1-a)>1-b,
所以
 是“好函数”;
是“好函数”;③设a、b、c∈(0,1)且a+b>c
(i)若a≤ln2且b≤ln2,则ea+eb≥2

∵ln2≥
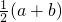 ,∴2≥
,∴2≥ 即2≥
即2≥
由此可得ea+eb≥

 =ea+b>ec
=ea+b>ec(ii)若a、b中至少有一个大于ln2,不妨设a>ln2
则ea+eb>eln2+e0=2+1=3,而ec<e1<3
∴ea+eb>ec,
综上所述,得ea+eb>ec,同理可得eb+ec>ea,ec+ea>eb.
因此f(x)=ex,x∈(0,1),是“好函数”;
④设a、b、c∈(0,π),取a=
 ,b=
,b= ,c=
,c=
得sina=sinb=
 ,sinc=1.虽然a+b>c,但是sina+sinb=sinc,
,sinc=1.虽然a+b>c,但是sina+sinb=sinc,不满足“好函数”的定义,故f(x)=sinx,x∈(0,π),不是“好函数”.
故选:B
点评:本题给出“好函数”的定义,要我们找出满足条件的函数.着重考查了基本初等函数的性质、不等式的证明和简单的演绎推理等知识,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
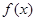 称为“好函数”:对于在
称为“好函数”:对于在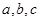 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则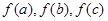 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数:  ②
②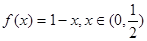
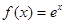 ,
,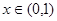 ④
④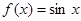 ,
, .
.