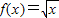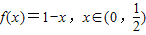题目内容
我们把具有以下性质的函数f(x)称为“好函数”:对于在f(x)定义域内的任意三个数a,b,c,若这三个数能作为三角形的三边长,则f(a),f(b),f(c)也能作为三角形的三边长.现有如下一些函数:
①f(x)=
②f(x)=1-x,x∈(0,
)
③f(x)=ex,x∈(0,1)
④f(x)=sinx,x∈(0,π).
其中是“好函数”的序号有
①f(x)=
| x |
②f(x)=1-x,x∈(0,
| 1 |
| 2 |
③f(x)=ex,x∈(0,1)
④f(x)=sinx,x∈(0,π).
其中是“好函数”的序号有
①②③
①②③
.分析:任给三角形,设它的三边长分别为a,b,c,则a+b>c,
①
+
>
>
,可得函数f(x)是“好函数”;
②作差,验证f(a)+f(b)>f(c),可得函数f(x)是“好函数”;
③ea+eb>2
=2
,若2
>ec,即ec<4,由c∈(0,1),可得结论成立;
④若f(a)+f(b)=sina+sinb=2sin
cos
>sinc,结论不一定成立.
①
| a |
| b |
| a+b |
| c |
②作差,验证f(a)+f(b)>f(c),可得函数f(x)是“好函数”;
③ea+eb>2
| ea+b |
| ec |
| ec |
④若f(a)+f(b)=sina+sinb=2sin
| a+b |
| 2 |
| a-b |
| 2 |
解答:解:任给三角形,设它的三边长分别为a,b,c,不妨设c是最大边,且a+b>c
①f(x)=
,∵
+
>
>
,∴函数f(x)是“好函数”;
②f(x)=1-x,∵f(a)+f(b)-f(c)=1+c-(a+b),a,b,c∈(0,
),∴f(a)+f(b)-f(c)>0,∴f(a)+f(b)>f(c),∴函数f(x)是“好函数”;
③f(x)=ex,ea+eb>2
=2
,若2
>ec,即ec<4,∵c∈(0,1),∴结论成立,∴函数f(x)是“好函数”;
④f(x)=sinx,若f(a)+f(b)=sina+sinb=2sin
cos
>sinc,则∵x∈(0,π),-π<a-b<c,∴结论不一定成立,∴函数f(x)不是“好函数”;
故答案为:①②③
①f(x)=
| x |
| a |
| b |
| a+b |
| c |
②f(x)=1-x,∵f(a)+f(b)-f(c)=1+c-(a+b),a,b,c∈(0,
| 1 |
| 2 |
③f(x)=ex,ea+eb>2
| ea+b |
| ec |
| ec |
④f(x)=sinx,若f(a)+f(b)=sina+sinb=2sin
| a+b |
| 2 |
| a-b |
| 2 |
故答案为:①②③
点评:本题主要考查进行简单的合情推理、三角函数的性质等基础知识,考查运算求解能力,考查化归与转化思想,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
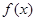 称为“好函数”:对于在
称为“好函数”:对于在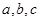 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则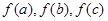 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数:  ②
②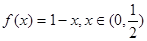
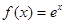 ,
,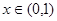 ④
④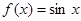 ,
, .
.