题目内容
椭圆
+
=1(a>2)的右焦点为F,直线x=m与椭圆相交于 A、B两点,直线x=m不过右焦点F时,△FAB的周长的最大值是16,则该椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| 4 |
分析:设椭圆的左焦点为E,作出图形,利用椭圆的定义可求得△FAB的周长l=AB+AF+BF=4a+AB-AE-BE≤4a=16,从而可求得a,继而可得其离心率.
解答: 解:设椭圆的左焦点为E,
解:设椭圆的左焦点为E,
△FAB的周长l=AB+AF+BF=AB+(2a-AE)+(2a-BE)=4a+AB-AE-BE,
∵AE+BE≥AB,
∴AB-AE-BE≤0,当且仅当AB过E时取到“=”,
∴AB+AF+BF=4a+AB-AE-BE≤4a(当且仅当AB过E时取到“=”),
即直线x=m过椭圆左焦点E时△FAB的周长最大.
∵△FAB的周长的最大值是16,
∴4a=16,
∴a=4,a2=16,又b2=4,
∴c2=a2-b2=16-4=12,
该椭圆的离心率e=
=
=
.
故选A.
 解:设椭圆的左焦点为E,
解:设椭圆的左焦点为E,△FAB的周长l=AB+AF+BF=AB+(2a-AE)+(2a-BE)=4a+AB-AE-BE,
∵AE+BE≥AB,
∴AB-AE-BE≤0,当且仅当AB过E时取到“=”,
∴AB+AF+BF=4a+AB-AE-BE≤4a(当且仅当AB过E时取到“=”),
即直线x=m过椭圆左焦点E时△FAB的周长最大.
∵△FAB的周长的最大值是16,
∴4a=16,
∴a=4,a2=16,又b2=4,
∴c2=a2-b2=16-4=12,
该椭圆的离心率e=
| c |
| a |
2
| ||
| 4 |
| ||
| 2 |
故选A.
点评:本题考查椭圆的简单性质,着重考查椭圆的定义的应用,考查不等式的作用,求得a=4是关键,属于中档题.

练习册系列答案
相关题目
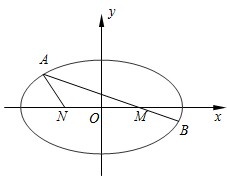 如图,已知椭圆
如图,已知椭圆