题目内容
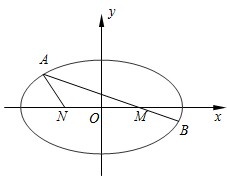 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| 4 |
(1)若tan∠ANM=-2,tan∠AMN=
| 1 |
| 2 |
(2)若
| MA |
| MB |
分析:(1)根据tan∠ANM=-2,tan∠AMN=
,得直线AM和AN的直线方程,将此二方程联立解得x和y,可知点A的坐标,根据A在椭圆上,求得a,进而求得椭圆方程可得.
(2)利用向量的坐标公式得出
,
的坐标,结合条件
=-2
得出坐标间的关系,又根据A,B两点的坐标适合椭圆方程得出x1-2x2=-a2,从而建立建立a的不等关系,求得a的取值范围,即可解得椭圆的离心率e的取值范围.
| 1 |
| 2 |
(2)利用向量的坐标公式得出
| MA |
| MB |
| MA |
| MB |
解答:解:(1)由题意得,直线AN的斜率k1=tan∠ANM=-2,AM的斜率k2=-tan∠AMN=-
,
所以直线AN的方程为y=-2(x+1),同理直线AM的方程为:y=-
(x-1),
联立两直线方程,解得点A的坐标为(-
,
),
因为A在椭圆上,所以
+
=1,a2=5,
∴该椭圆的方程
+
=1;
(2)
=(x1-1,y1),
=(x2-1,y2),
∵若
=-2
,∴
即
.
又∵
+
=1①;
+
=1②;
∴①-②×4得:(x1+2x2)(x1-2x2)=-3a2,
∴x1-2x2=-a2,从而x1=
(3-a2),x2=
(3+a2),
∵0<x1<x2,∴
(3-a2)>0,
(3-a2)<
(3+a2),
解得:1<a<
,
e2=
∈(
,
),
∴e∈(
,
),
∴椭圆的离心率e的取值范围(
,
).
| 1 |
| 2 |
所以直线AN的方程为y=-2(x+1),同理直线AM的方程为:y=-
| 1 |
| 2 |
联立两直线方程,解得点A的坐标为(-
| 5 |
| 3 |
| 4 |
| 3 |
因为A在椭圆上,所以
| 5 2 |
| 9a 2 |
| 4 2 |
| 9×4 |
∴该椭圆的方程
| x 2 |
| 5 |
| y2 |
| 4 |
(2)
| MA |
| MB |
∵若
| MA |
| MB |
|
|
又∵
| x1 2 |
| a 2 |
| y1 2 |
| 4 |
| x 22 |
| a 2 |
| y2 2 |
| 4 |
∴①-②×4得:(x1+2x2)(x1-2x2)=-3a2,
∴x1-2x2=-a2,从而x1=
| 1 |
| 2 |
| 1 |
| 4 |
∵0<x1<x2,∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解得:1<a<
| 3 |
e2=
| 4-a 2 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
∴e∈(
| 1 |
| 2 |
| ||
| 2 |
∴椭圆的离心率e的取值范围(
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查直线与圆锥曲线的综合问题、椭圆的概念和性质、直线方程以及综合应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
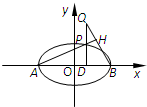 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆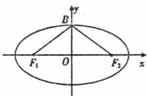 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆