题目内容
设a∈R,f(x)=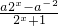 为奇函数.
为奇函数.
(1)求实数a的值;
(2)设g(x)=2log2( ),若不等式f-1(x)≤g(x)在区间[
),若不等式f-1(x)≤g(x)在区间[ ,
, ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围.
解:(1)f(x)=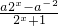 =a-
=a-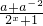
由f(x)是奇函数,可得f(-x)=-f(x),
∴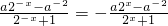
∴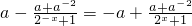
∴2a=a+a-2
∴a=1,
∴f(x)=
(2)由y=f(x)= 可得
可得 ,∴
,∴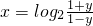 ,∴f-1(x)=
,∴f-1(x)=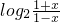 ,
,
不等式f-1(x)≤g(x)在区间[ ,
, ]上恒成立,即
]上恒成立,即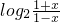 ≤2log2(
≤2log2( )恒成立,
)恒成立,
即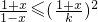 恒成立
恒成立
即k2≤1-x2在区间[ ,
, ]上恒成立,
]上恒成立,
∵y=1-x2在区间[ ,
, ]上单调递减
]上单调递减
∴
∴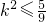
∴ .
.
分析:(1)f(x)=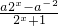 =a-
=a-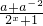 ,由f(x)是奇函数,可得f(-x)=-f(x),代入化简可求实数a的值;
,由f(x)是奇函数,可得f(-x)=-f(x),代入化简可求实数a的值;
(2)由y=f(x)= 可得f-1(x)=
可得f-1(x)=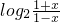 ,不等式f-1(x)≤g(x)在区间[
,不等式f-1(x)≤g(x)在区间[ ,
, ]上恒成立,即
]上恒成立,即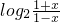 ≤2log2(
≤2log2( )恒成立,即k2≤1-x2在区间[
)恒成立,即k2≤1-x2在区间[ ,
, ]上恒成立,求出右边函数的最小值,即可求实数k的取值范围.
]上恒成立,求出右边函数的最小值,即可求实数k的取值范围.
点评:本题考查函数的奇偶性,考查反函数,考查恒成立问题,解题的关键是分离参数,确定函数的最值,属于中档题.
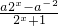 =a-
=a-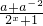
由f(x)是奇函数,可得f(-x)=-f(x),
∴
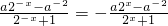
∴
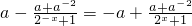
∴2a=a+a-2
∴a=1,
∴f(x)=

(2)由y=f(x)=
 可得
可得 ,∴
,∴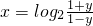 ,∴f-1(x)=
,∴f-1(x)=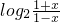 ,
,不等式f-1(x)≤g(x)在区间[
 ,
, ]上恒成立,即
]上恒成立,即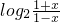 ≤2log2(
≤2log2( )恒成立,
)恒成立,即
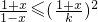 恒成立
恒成立即k2≤1-x2在区间[
 ,
, ]上恒成立,
]上恒成立,∵y=1-x2在区间[
 ,
, ]上单调递减
]上单调递减∴

∴
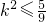
∴
 .
.分析:(1)f(x)=
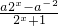 =a-
=a-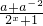 ,由f(x)是奇函数,可得f(-x)=-f(x),代入化简可求实数a的值;
,由f(x)是奇函数,可得f(-x)=-f(x),代入化简可求实数a的值;(2)由y=f(x)=
 可得f-1(x)=
可得f-1(x)=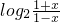 ,不等式f-1(x)≤g(x)在区间[
,不等式f-1(x)≤g(x)在区间[ ,
, ]上恒成立,即
]上恒成立,即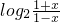 ≤2log2(
≤2log2( )恒成立,即k2≤1-x2在区间[
)恒成立,即k2≤1-x2在区间[ ,
, ]上恒成立,求出右边函数的最小值,即可求实数k的取值范围.
]上恒成立,求出右边函数的最小值,即可求实数k的取值范围.点评:本题考查函数的奇偶性,考查反函数,考查恒成立问题,解题的关键是分离参数,确定函数的最值,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目