题目内容
已知cosα= ,cos(α+β)=-
,cos(α+β)=- ,α、β∈(0,
,α、β∈(0, ),求β.
),求β.
解:∵cosα= ,cos(α+β)=-
,cos(α+β)=- ,
,
∴sinα= =
=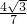 ,sin(α+β)=
,sin(α+β)= =
=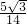
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinβ= ,
,
∴β= .
.
分析:先利用已知条件求得sinα和sin(α+β)的值,进而利用cosβ=cos[(α+β)-α]根据两角和公式展开,求得答案.
点评:本题主要考查了两角和与差的余弦函数,同角三角函数基本关系的应用.注意对三角函数基本公式的熟练记忆.
 ,cos(α+β)=-
,cos(α+β)=- ,
,∴sinα=
 =
=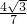 ,sin(α+β)=
,sin(α+β)= =
=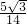
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinβ=
 ,
,∴β=
 .
.分析:先利用已知条件求得sinα和sin(α+β)的值,进而利用cosβ=cos[(α+β)-α]根据两角和公式展开,求得答案.
点评:本题主要考查了两角和与差的余弦函数,同角三角函数基本关系的应用.注意对三角函数基本公式的熟练记忆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,
(2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,