Question

【题目】如图所示，在四边形中：，，，，．点为四边形的外接圆劣弧（不含）上一动点．

（1）证明：；

（2）若，设，，求的最小值．

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）由余弦定理求得，再根据，求得，最后根据三边长度判断是否满足勾股定理；

（2）设交于，作平行于且交于，则四边形为平行四边形，由平面向量基本定理和正弦定理表示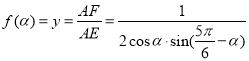，再根据三角恒等变形求的最小值.

解：（1）在中，由余弦定理知：

所以，又因为，所以

所以分别为方程的两根，

因为，所以

所以，所以

（2）因为，所以是四边形的外接圆的直径，

所以四边形为矩形，连接，

设交于，作平行于且交于，则四边形为平行四边形，

所以，又因为，

由平面向量基本定理知：，所以

在中，因为，，所以

由正弦定理知：，所以

在中，

所以，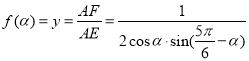

所以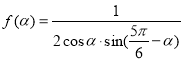

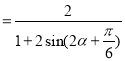
因为，所以，所以

所以，当时，取最小值，最小值为．