Question

【题目】 已知抛物线，过焦点的动直线交抛物线于两点，抛物线在两点处的切线相交于点.（Ⅰ）求的值；（Ⅱ）求点的纵坐标；

Answer 1

【答案】(1) ,(2) 点 的纵坐标为 ..

【解析】试题分析：（I）设直线l的方程为．将它与抛物线的方程联立组成方程组，消去y得到关于x的二次方程，再结合根与系数的关系即可求出的值；

（II）利用导数几何意义求出切线的斜率，从而求得切线的方程，最后联立直线的方程组成方程组求出交点Q的坐标即可

（Ⅰ）解： ，又依题意直线不与轴垂直，

∴设直线的方程为.

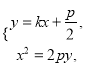由可得.

设，

.

(Ⅱ)解：由，可得 ，

∴抛物线在 两点处的切线的斜率分别为 .

∴在点A处的切线方程为 ,

同理在点B处的切线方程为.

解方程组 可得 ,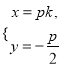

即点的纵坐标为 .