题目内容
(本题满分12分)在如图的多面体中, ⊥平面
⊥平面 ,
,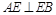 ,
,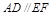 ,
,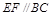 ,
,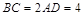 ,
,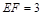 ,
,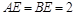 ,
,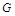 是
是 的中点.
的中点.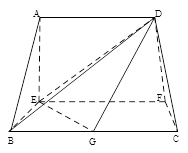
(Ⅰ) 求证: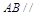 平面
平面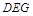 ;
;
(Ⅱ) 求证: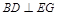 ;
;
(Ⅲ) 求二面角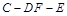 的余弦值.
的余弦值.
解析试题分析: 解:(Ⅰ)证明:∵
解:(Ⅰ)证明:∵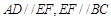 ,∴
,∴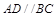 ; 又∵
; 又∵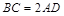 ,
,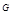 是
是 的中点,∴
的中点,∴ ,且
,且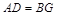 ,∴四边形
,∴四边形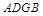 是平行四边形,∴
是平行四边形,∴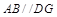 . ∵
. ∵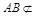 平面
平面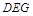 ,
, 平面
平面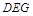 ,∴
,∴ 平面
平面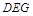 . 4分
. 4分
(Ⅱ) 解法1:证明:∵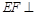 平面
平面 ,
, 平面
平面 ,∴
,∴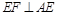 ;又
;又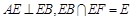 ,
,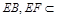 平面
平面 ,∴
,∴ 平面
平面 . 过
. 过 作
作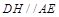 交
交 于
于 ,则
,则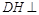 平面
平面 .∵
.∵ 平面
平面 ,∴
,∴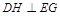 .
.
∵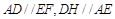 ,∴四边形
,∴四边形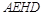 平行四边形,∴
平行四边形,∴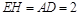 ,∴
,∴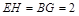 ,又
,又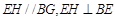 ,∴四边形
,∴四边形 为正方形,∴
为正方形,∴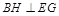 ,又
,又 平面
平面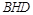 ,
,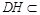 平面
平面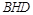 ,∴
,∴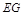 ⊥平面
⊥平面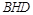 . ∵
. ∵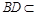 平面
平面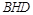 ,∴
,∴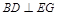 . 8分
. 8分
解法2:∵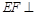 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,∴
,∴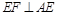 ,
,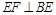 ,
, 又
又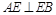 ,∴
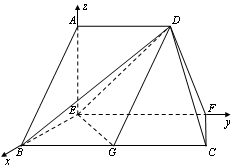
,∴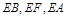 两两垂直. 以点
两两垂直. 以点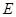 为坐标原点,
为坐标原点,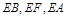 分别为
分别为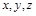 轴建立如图所示的空间直角坐标系. 由已知得,
轴建立如图所示的空间直角坐标系. 由已知得, ,
,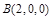 ,
,
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF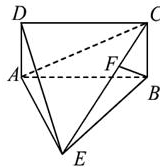
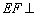 平面AEB,
平面AEB, ,
, ,
,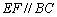 ,
,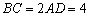 ,
,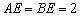 ,
, ,G是BC的中点.
,G是BC的中点.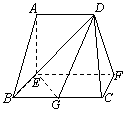
 ;
; 的大小.
的大小.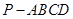 中,
中,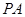 ⊥平面
⊥平面 ,
, 为
为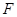 为
为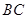 的中点,底面
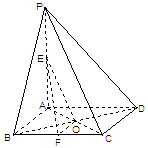
的中点,底面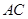 ,
, 交于点
交于点 .
.
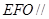 平面
平面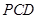 ;
; ⊥平面
⊥平面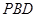 .
.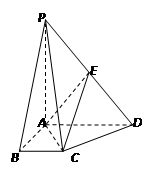

 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱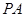 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点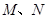 分别是
分别是 的中点.求
的中点.求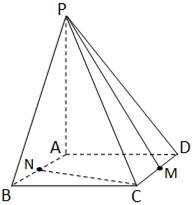
 与
与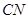 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);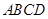 所在平面与平面四边形
所在平面与平面四边形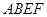 所在平面互相垂直,△
所在平面互相垂直,△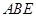 是等腰直角三角形,
是等腰直角三角形,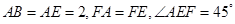
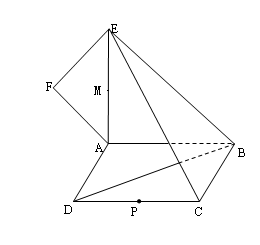
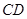 的中点为
的中点为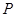 ,线段
,线段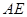 的中点为
的中点为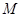 ,求证:
,求证: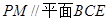 ;
;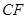 与平面
与平面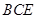 所成角的正切值.
所成角的正切值.