题目内容
16.命题“对任意x>0,都有2x>1”的否定是存在x>0,有2x≤1.分析 根据全称命题的否定是特称命题进行求解.
解答 解:命题为全称命题,则命题的否定是:存在x>0,有2x≤1,
故答案为:存在x>0,有2x≤1.
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
4.要得到函数y=2sin(2x+$\frac{π}{3}$)的图象,只需将函数y=2sinx的图象上所有点( )
| A. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| B. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| D. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) |
5.过曲线y=3x-x3上一点A(2,-2)的切线方程为( )
| A. | y=-2 | B. | 9x+y+16=0 | C. | 9x+y-16=0 | D. | 9x+y-16=0或y=-2 |
6.在△ABC中,a、b、c分别是角A、B、C的对边,a=1,△ABC的面积为$\frac{\sqrt{3}}{2}$,f(x)=2sin(2x+$\frac{π}{6}$)+1,且f(B)=2,则$\frac{b}{sinB}$的值为( )
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{7}$ | D. | 4 |
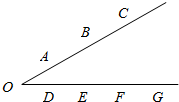 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.